Cache Models and Program Transformations

Memory Wall Problem

Optimization focus so far has been reducing the amount of computation. However, on modern machine, most programs that access a lot of data are memory bound. The latency of DRAM is usually on the order of 100-1000 cycles.

Caches can reduce the effective latency of memory access, but programs may need to be rewritten to take full advantage of caches.

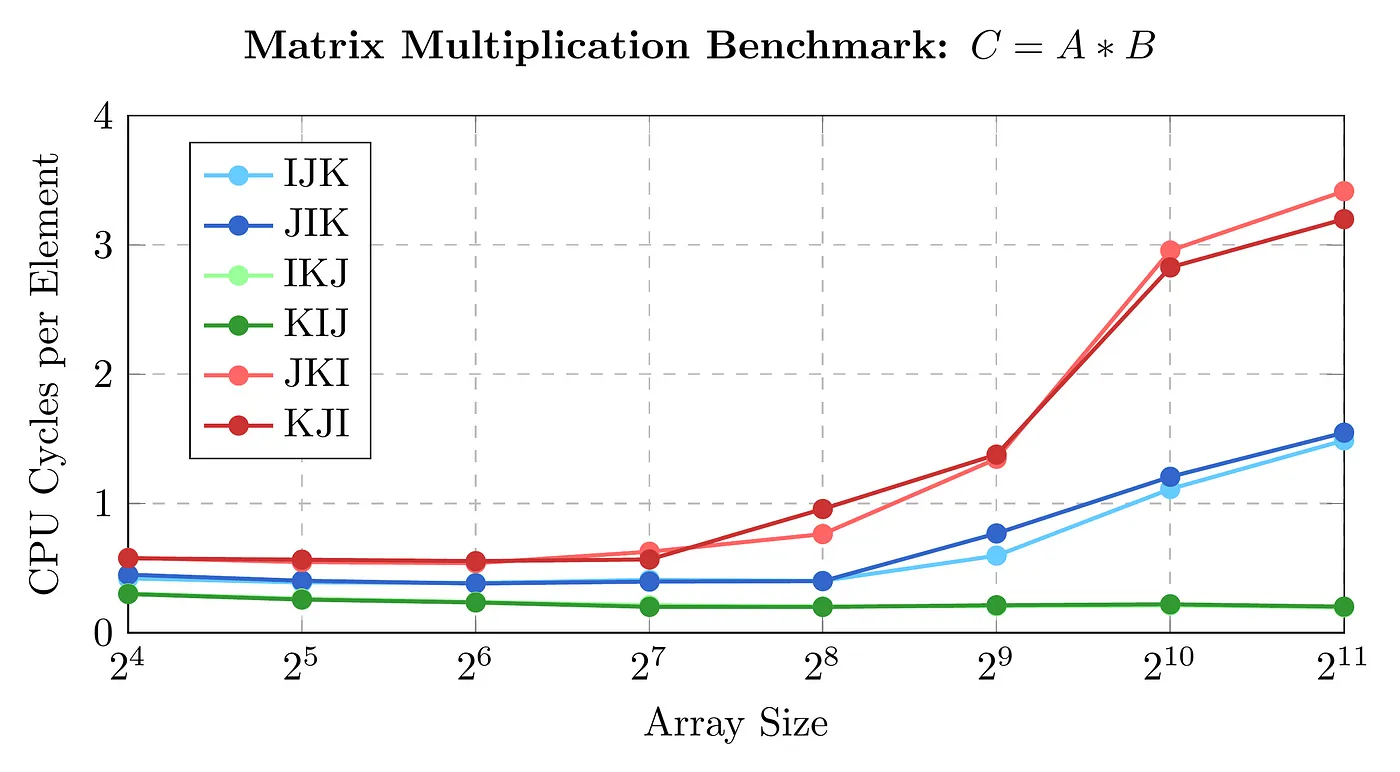
Do Cache Optimizations Matter?

This is best shown by way of Matrix Multiplication. Because matrix multiplication requires multiple passes over the same memory addresses, there is a lot of space for cache optimization.

https://medium.com/@Styp/why-loops-do-matter-a-story-of-matrix-multiplication-cache-access-patterns-and-java-859111845c25

Two Key Transformations

Loop Interchange/Permutation

for I ...
	for J ...
		S(I,J);

could possibly become:

for J'
	for I'
		S'(I',J')

Loop Tiling/Blocking

Intuition: interleave I and J executions:

for I...
	for J...
		S(I,J)

could possibly become:

for BI...
	for BJ...
		for I'
			for J'
				S'(BI,BJ,I',J')

Questions

Are these transformations legal?

Is it profitable to perform these transformations?

Is it profitable to perform these transformations?

If so, how can we perform them?

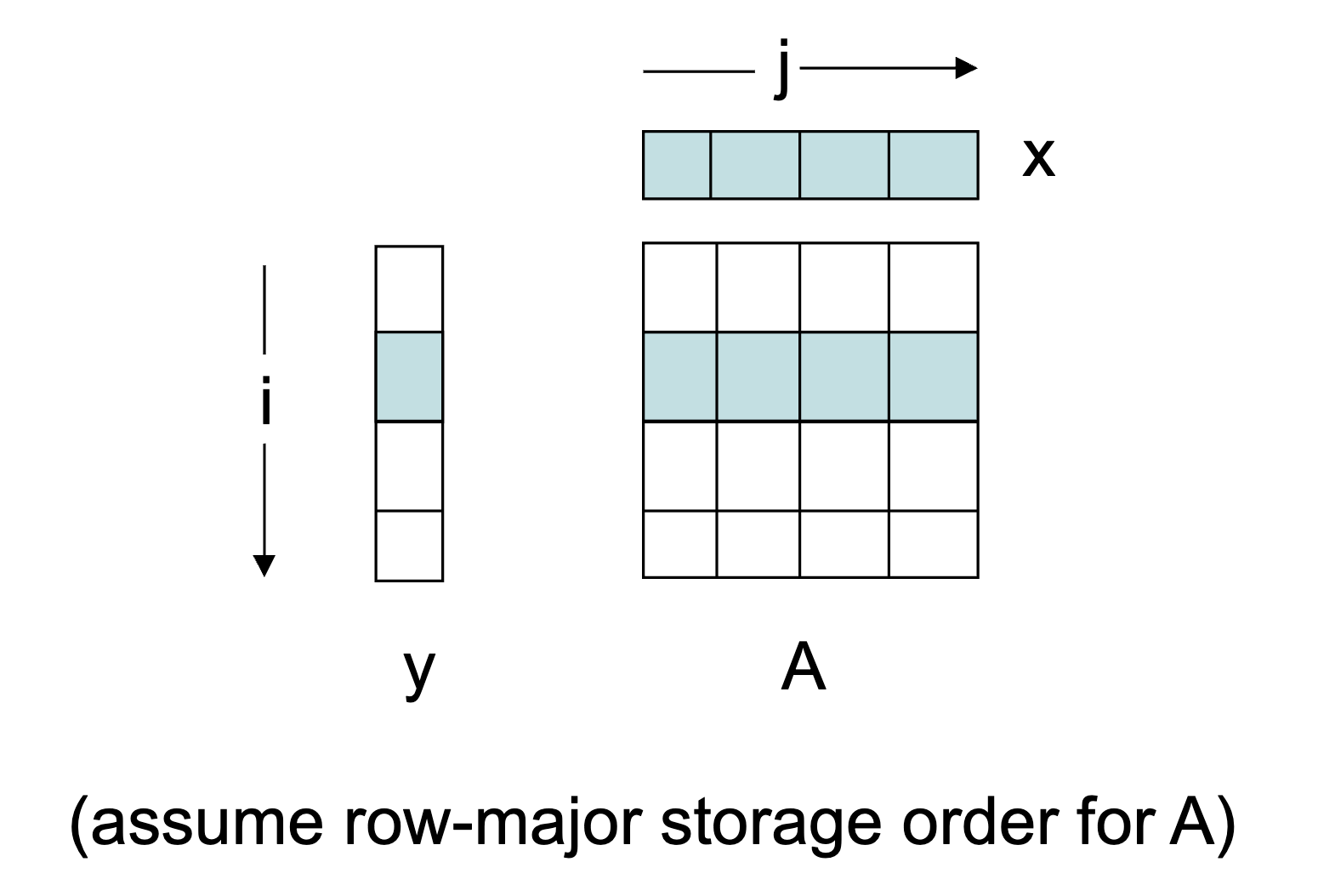
Matrix-Vector Product

Imagine the following code:

for i = 1,N
	for j = 1,N
		y(i) = y(i) + A(i,j) * x(j)

https://www.cs.utexas.edu/~pingali/CS380C/2025/lectures/Cache%20Models.pdf

Cache Abstractions

Real caches are very complex, science is all about tractable and useful abstractions (models) of complex phenomena—models are usually approximations. We’ll assume a two level memory model: single-level-cache + memory.

Stack Distance

Lets say $r_1$ and $r_2$ are two memory references where $r_1$ occurs earlier than $r_2$. $\text{stackDistance}(r_1,r_2)$: number of distinct cache lines referenced between $r_1$ and $r_2$.

Modeling Approach

Our first approximation is to ignore conflict misses and only consider cold and capacity misses.

Most problems have the notion of problem size. How does the cache miss ratio change as we increase problem size?

We can often estimate miss ratios at two extremes:

• Large Cache Model: problem size is small compared to cache capacity
• Small Cache Model: problem size is large compared to cache capacity

Large Cache Model

No capacity misses, only cold misses.

Small Cache Model

Cold misses and capacity misses.

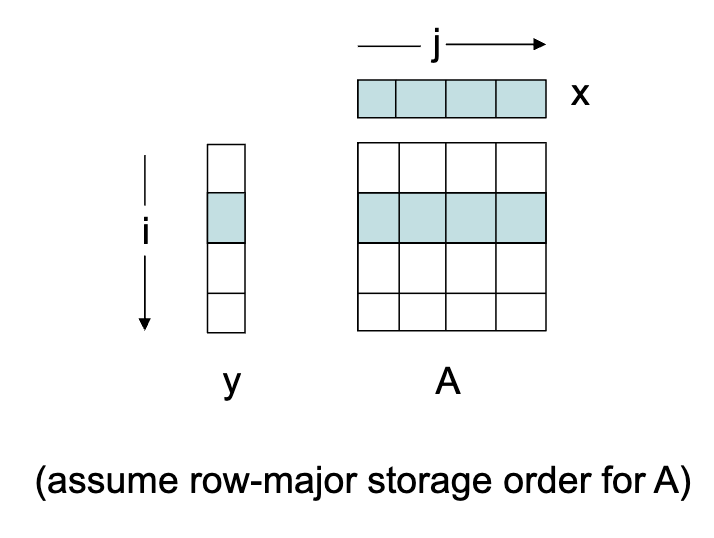
Scenario 1

Lets say we have an IJ loop for performing Matrix-vector products.

The cache line size is 1 number.

In the large cache model, we have $N^2$ misses to A, $N$ misses to y, and $N$ misses to x. The total is $N^2+2N$, so the miss ratio is $\frac{N^2+2N}{4N^2}$ which is about $\approx 0.25+\frac{0.5}{N}$.

In the small cache model, we have $N^2$ misses to A, $N$ misses to y, and $N+(N-1)$ misses to x. The total is $2N^2+N$, so the miss ratio is $\frac{2N^2+N}{4N^2}$ which is about $\approx 0.5+\frac{0.25}{N}$.

As the problem size increases, when do capacity misses start to occur? This depends on the replacement policy, the most common is LRU or Pseudo LRU (PLRU).

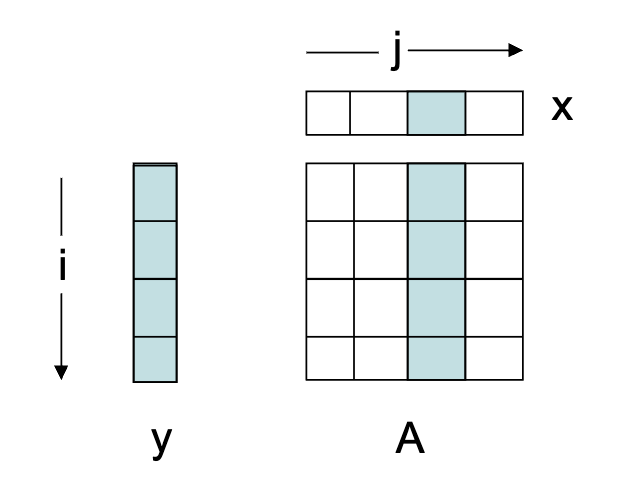
Scenario 2

Lets say we have a JI loop for performing Matrix-vector products.

The miss ratio is the exact same as it was in scenario 1 because the roles of x and y are just interchanged, but the cache line size is simply for a single memory location as defined in scenario 1.

https://www.cs.utexas.edu/~pingali/CS380C/2025/lectures/Cache%20Models.pdf

Scenario 3

Say we have the same thing but the cache line size is $b$ numbers.

https://www.cs.utexas.edu/~pingali/CS380C/2025/lectures/Cache%20Models.pdf

In the large cache model, we have:

• A: $\frac{N^2}{b}$ misses
• x: $\frac{N}{b}$ misses
• y: $\frac{N}{b}$ misses
• Total: $\frac{N^2+2N}{b}$ misses
• Miss ratio: $\frac{N^2+2N}{4b{N}^2}\approx \frac{0.25}{b}+\frac{0.5}{bN}$